הכללה של IMO 1995/6 ומשפט Wolstenholme (חלק 1/2)

שלום קוראים,

אני אמשיך את הקו הקומבינטורי-אלגברי של הפוסט הקודם, אבל עם משהו אלמנטרי יותר.
הפעם נעסוק בבעיית ספירה עם ניחוח של תורת המספרים. בחלק זה מתוך סדרה של 2 פוסטים נפתור את בעית הספירה ב-3 דרכים, נכליל אותה ונפתור שוב, ואז נפרוש איש איש לענייניו.

בפוסט הבא נעסוק במשפט קשור (קונגרואנציה יפה שמוסברת באמת רק מתוך אנליזה $p$ -אדית), ועל הכללה מסוימת שלו שהוכחתי לבקשת זוכה מדליית פילדס. בחיי שאני לא משקר. חכו לפוסט הבא…

0. הבעיה

הבעיה שאעסוק בה היא הבעיה השישית והאחרונה (כלומר, הקשה ביותר) בתחרות המתמטיקה הבינלאומית (International Mathematical Olympiad, או בקיצור: IMO) ה-36. היא התקיימה בטורונטו, קנדה ב-1996. מתוך 412 משתתפים, 34 פתרו את הבעיה (לשם השוואה, הבעיה השנייה ברמת הקושי שלה, שהייתה באותה שנה הבעיה השנייה מבחינה כרונולוגית, נפתרה ע"י 90 מתמודדים).

למי שלא מכיר, ה-IMO היא תחרות יוקרתית במתמטיקה המיועדת לנוער (יש הגבלת גיל) ומתקיימת מדי שנה. כל מדינה רשאית לשלוח עד 6 נציגים, שמתחרים במשך יומיים באופן אישי בפיתרון 6 שאלות: 3 שאלות ביום הראשון, ו-3 שאלות ביום השני, כאשר הזמן המוקצב בכל יום הוא 4.5 שעות. השאלות בכל יום מסודרות בסדר קושי עולה (או כך לפחות אמור להיות; בפועל לא תמיד קורה). כל משתתף מקבל ציון על פתרונותיו, כאשר הציון המקסימלי האפשרי הוא 42: כל שאלה שווה עד 7 נקודות. על אף הקושי הרב של הבעיות, הן הניסוח והן הפיתרון משתמשים בידע תיכוני בלבד – למרות שידע על-תיכוני לא יכול להזיק, בלשון המעטה.
(למקרה שאתם תוהים, אני כמובן לא השתתפתי באותו IMO; הייתי בן 4.5. מבינים? הייתי כ"כ צעיר שעוד ספרתי את הגיל שלי בחצאים.)

ניגש לבעיה:

יהי $p$ ראשוני אי-זוגי. כמה תתי-קבוצות של $\{1,2,\cdots, 2p\}$ יש, כך שמספר האיברים בקבוצה הוא $p$ וסכום האיברים בקבוצה מתחלק ב- $p$ ?

בעית ספירה, מאוד קונקרטית, מאוד אלגנטית. אילולא הנתון על הראשוניות של $p$ , לא היה ברור שיש בכלל קשר חזק לתורת המספרים – אבל יש. אפריורי גם לא ברור למה רלוונטי הנתון? מה קורה אם מנסים לפתור את השאלה הכללית? ובכן, "אספיילר" ואגיד שהחשיבות היחידה של הנתון היא פישוט השאלה. ללא נתון זה, השאלה קשה יותר. כאשר נפתור את המקרה הכללי נראה מדוע המקרה של $p$ ראשוני הוא הפשוט ביותר.

אנקדוטה על המחבר: מחבר השאלה הוא Marcin Kuczma, מתמטיקאי פולני שהשתתף בעצמו ב-IMO בתחילת שנות ה-60'. הוא אימן את הנבחרת הפולנית בשנים מסוימות, והציע שאלות רבות ל-IMO, ובשנים 1983, 1989, 1995 ו-1999 שאלות שלו אף התקבלו לתחרות עצמה. למעשה, ב-1995 התקבלה שאלה נוספת שלו לתחרות מלבד השאלה בה עוסק הפוסט – השאלה הרביעית.

1. הוכחות

אתן 3 הוכחות: אחת קומבינטורית, ושתיים אלגבריות. אני מדגיש שאלו אינם פתרונות שלי אלא פתרונות מפורסמים לבעיה.

הוכחה קומבינטורית

(זו ההוכחה המקורית של מחבר השאלה.) נתחיל עם האינטואיציה. יש $\binom{2p}{p}$ תתי-קבוצות בגודל $p$ . אנחנו מחפשים בתוכן את הקבוצות שסכומן מתחלק ב- $p$ . הרעיון הוא שהסכום מודולו $p$ מתפלג באופן כמעט אחיד. אפשר להראות זאת אם נצליח לחלק את (רוב) המרחב לאוספים זרים בגודל $p$ , כאשר בכל אוסף מופיעות כל האפשרויות לסכום מודולו $p$ .

יש כמה דרכים לקבל חלוקה כזו. אתן דוגמא לחלוקה, ואז אסביר בשפה קצת יותר גבוהה מה מוביל לחלוקה כזו. החלוקה הולכת כך:
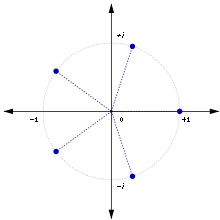
אנחנו רוצים לחלק את $A= \{ S \subseteq \{1,2,\cdots,2p\} \mid |S|=p\}$ . נתעלם לרגע מ-2 קבוצות: $\{1,2,\cdots ,p\}$ ו- $\{p+1,p+2,\cdots,2p\}$ . עבור קבוצה $S_0 \in A$ ששונה מהשתיים שהזכרתי, אגדיר שיהיו איתה בחלוקה כל הקבוצות המתקבלות מ"סיבוב" החצי הראשון שלה, כלומר: סיבוב של החיתוך שלה עם $\{1,2,3,\cdots, p\}$ . אסביר זאת בציור עבור $p=7$ :

(פשוט מוסיפים 1 לכל האיברים שקטנים שווים מ- $p$ , ואם מקבלים $p+1$ מחליפים אותו ב- $1$ .)
נשים לב לתכונה חשובה: הסכום של הקבוצות הללו שונה מודולו $p$ . הסיבה היא שסיבוב האיברים ב- $S_0 \cap \{ 1,2,\cdots, p\}$ ב- $\Delta$ משנה את הסכום מודולו $p$ ב- $\Delta \cdot s$ , כאשר $s$ הוא גודל החיתוך $|S_0 \cap \{ 1,2,\cdots, p\}|$ – מספר זר ל- $p$ (כאן משתמשים בראשוניות – מספר טבעי קטן מ- $p$ הוא בהכרח זר ל- $p$ ). הפונקציה $\Delta \mapsto \Delta \cdot s \mod p$ היא חח"ע ועל.

למה זה מסיים את השאלה? הראתי שאם מתעלמים מ-2 קבוצות ב- $S$ , הסכום מודולו $p$ מתפלג באופן אחיד. קל לראות שהסכום של איברי 2 הקבוצות יוצאות הדופן מתחלק ב- $p$ . על כן, יש $\frac{\binom{2p}{p}-2}{p} +2$ קבוצות שסכום איבריהן מתחלק ב- $p$ . למעשה, קיבלנו עוד מידע: יש $\frac{\binom{2p}{p}-2}{p}$ קבוצות שסכום איבריהן הוא $i \mod p$ , לכל $i \neq 0$ .

מה הוביל אותי לעניין הסיבובים? ובכן, הדרך הטבעית ביותר לבניית חלוקה היא למצוא איזושהי פעולה של החבורה הציקלית $C_p = \mathbb{Z}/p\mathbb{Z}$ על $A$ . בהינתן פעולה, אפשר להסתכל על המסלולים של הקבוצות ב- $A$ תחת הפעולה – זה נותן חלוקה של $A$ . אורך של מסלול יהיה לרוב $p$ , אלא אם מדובר בנקודת שבת של הפעולה ואז הוא יהיה באורך 1. אם נבחר את הפעולה בחוכמה, הסכומים של איברי הקבוצות בכל מסלול יהיו שונים מודולו $p$ , ונוכל לספור במדויק כמה קבוצות יש עם סכום נתון מודולו $p$ . מספר נקודות השבת הוא קריטי בחישוב, ובדיוק מסביר מה הסטייה של התשובה מ- $\frac{\binom{2p}{p}}{p}$ . אם בוחרים בפעולת "סיבוב החצי הראשון", יש 2 נקודות שבת – הקבוצות $\{1,2,\cdots ,p\}$ ו- $\{p+1,p+2,\cdots,2p\}$ . $\blacksquare$

הוכחה אלגברית

הפיתרון הבא הוא של Nikolay Nikolov, מתמודד בולגרי שהשתתף בתחרות. הוא פתר את כל השאלות וקיבל ציון מושלם של 42 נקודות. על הפיתרון הלא שגרתי שלו לבעיה השישית הוא קיבל בנוסף פרס מיוחד שניתן בדיוק במקרים בהם המתמודדים מצליחים להפתיע את מחברי השאלות עצמם. כיום הוא מתמטיקאי באוקספורד שמתעסק בחבורות מכל הסוגים.

שורשי יחידה (תמונת אילוסטרציה)

נחזור למתמטיקה. נסמן ב- $\omega$ שורש יחידה מסדר $p$ בדיוק. הרעיון הוא להסתכל על המכפלה $\prod_{i=1}^{2p} (x-\omega^i)$ . מצד אחד, היא שווה ל- $(\prod_{i=1}^{p} (x-\omega^i))^2 = (x^p-1)^2 = x^{2p}-2x^p+1$ . מצד שני, אם נפתח סוגריים נקבל שהמקדם של $x^{2p-j}$ שווה לסכום $\sum_{1 \le i_1 < i_2 < \cdots < i_j \le 2p} \omega^{\sum_{k} i_k}$ עד כדי הסימן $(-1)^j$ .

ע"י השוואת המקדם של $x^p$ בשתי דרכי ההסתכלות מקבלים $2 = \sum_{1 \le i_1 < i_2 < \cdots < i_p \le 2p} \omega^{\sum_{k} i_k}$ . בגלל שלשורשי יחידה יש מחזוריות ( $\omega^{p+k} = \omega^k$ ), אפשר לבטא את הסכום הגדול בתור $\sum_{i=0}^{p-1} a_i \omega^i$ באשר $a_i$ סופר כמה תתי-קבוצות בגודל $p$ של $\{1,2,\cdots, 2p\}$ יש כך שסכום איבריהן הוא $i \mod p$ . אנחנו מעוניינים ב- $a_0$ .

מסתבר שהשיוויון $\sum_{i=0}^{p-1} a_i \omega^i = 2$ מאפשר לנו לקבל מידע רב: הוא גורר שהפולינום $\sum a_i x^i - 2$ מתאפס על $\omega$ . זה פולינום ממעלה $p-1$ לכל היותר. מקריטריון איזנשטיין, ידוע ש- $1+x+\cdots +x^{p-1} = \frac{x^p-1}{x-1}$ הוא הפולינום המינימלי של $\omega$ , ולכן הפולינום $\sum a_i x^i - 2$ הוא בהכרח כפולה (בסקלר) של $1+x+\cdots+x^{p-1}$ . המשמעות של זה היא שהמקדמים של $\sum a_i x^i - 2$ שווים זה לזה:

$a_0-2=a_1=a_2=\cdots=a_{p-1}$

נשלב זאת עם כך שאנחנו יודעים את סכום המקדמים בגלל ש- $\sum a_i$ שווה למספר תתי-הקבוצות בגודל $p$ של $\{1,2,\cdots,2p\}$ , כלומר ל- $\binom{2p}{p}$ , ונקבל $a_0 = \frac{\binom{2p}{p}-2}{p}+2$ . $\blacksquare$

ניסוח שונה עם פונקציות יוצרות

בהמשך הפוסט נרצה להכליל את ההוכחה האחרונה. בשביל זה נוח יותר לנסח אותה עם פונקציות יוצרות. כשנעשה זאת נגלה שלא באמת צריך לדעת מה הפולינום המינימלי של שורש יחידה מסדר $p$ . זה מפוגג את עננת המיסטיקה מהפיתרון האחרון.

נגדיר את הפולינום $F(x,y) := \prod_{i=1}^{2p} (1+x^iy)$ . זו פונקציה יוצרת – המקדם של $x^i y^j$ סופר כמה תתי-קבוצות של $\{1,2,\cdots, 2p\}$ הן מגודל $j$ וסכום איבריהן הוא $i$ . נסמן מקדם זה ב- $a_{i,j}$ . אותנו מעניין $\sum_{i = 0 \mod p} a_{i,p}$ .

כדי להבין איך ניגשים לסכום כזה, מומלץ להכיר תוצאה בסיסית בפונקציות יוצרות, בשם "series multisection", שאומרת את הדבר הבא: בהינתן טור פורמלי $F(x) = \sum a_i x^i$ מעל המרוכבים, אפשר להביע את הטור $F_{a,m}(x):= \sum_{i \equiv a \mod m} a_i x^i$ באמצעות הטור המקורי באופן הבא:

$F_{a,m}(x) = \frac{1}{m} \sum_{k=0}^{m-1} \omega_m^{-ak}F(x \omega_m^{k})$

באשר $\omega_m$ שורש יחידה פרימיטיבי מסדר $m$ . איך מוכיחים זהות זו? השוואת מקדמים בשני האגפים, ונוסחה לסכום סדרה גיאומטרית. שום דבר מעבר – מותיר לכם את החישוב. הדוגמה הכי פשוטה לעיקרון הזה היא השיוויון $\frac{F(x)+F(-x)}{2} = \sum a_{2i} x^{2i}$ .

נפעיל את התוצאה על הטור $F$ עם $(a,m)=(0,p)$ , כאשר חושבים על $F$ כטור במשתנה $x$ עם מקדמים שהם טורים ב- $y$ . נקבל:

$\sum_{i \equiv 0 \mod p, j \ge 0} a_{i,j} x^{i} y^{j} = \frac{1}{p} \sum_{i=0}^{p-1} F(x\omega_p^i, y)$

אם נציב $x=1$ , נקבל באגף שמאל ביטוי קרוב למה שאנחנו רוצים:

$\sum_{i \equiv 0 \mod p, j \ge 0} a_{i,j} y^{j} = \frac{1}{p} \sum_{i=0}^{p-1} F(\omega_p^i, y)$

אפשר להבין את המחוברים עם קצת עבודה:
למה: $F(1,y)=(1+y)^{2p}$ ו- $F(\omega_p^i,y) =(y^p+1)^2$ אם $p \nmid i$ . הוכחה: תרגיל. $\blacksquare$

נובע מייד ש-

$\sum_{i \equiv 0 \mod p, j \ge 0} a_{i,j} y^{j} = \frac{1}{p} ((p-1)(y^p+1)^2+(y+1)^{2p}))$

אנחנו רוצים את המקדם של $y^p$ . פותחים סוגריים עם הבינום של ניוטון ומקבלים $\frac{(p-1)2 + \binom{2p}{p}}{p}$ . $\blacksquare$

מה שאני אוהב בגישה הזו היא שהיא מאוד ישירה וברורה, במיוחד למי שמכיר קצת פונקציות יוצרות. היא לא דורשת רעיון עמוק, אלא הבנה של הסיטואציה שמאפשרת כתיבת הפונקציה היוצרת המתאימה $F$ ואז קצת אלגברה בשביל לחלץ ממנה את המידע הרצוי.

אציין וריאציה קטנה על הגישה: אפשר להשתמש ב-multisection "דו-מימדי"/כפול כדי לקבל ש- $\sum_{i \equiv 0 \mod p, j \equiv 0 \mod p} a_{i,j} = \frac{1}{p^2} \sum_{i,j=0}^{p-1} F(\omega_p^i, \omega_p^j)$ , ואפשר לחשב מפורשות את המחוברים. בסכום הזה מחשבים לא רק את המקרה $j=p$ אלא גם את $j=0,2p$ – ולכן צריך לחסר איזשהו מספר מהתוצאה (המספר הוא 2). בגישה זו של multisection אשתמש בהכללה בפרק הבא.

2. הכללה

נרצה לענות שאלה כללית יותר: כמה תתי-קבוצות של $\{1,2,\cdots, 2n\}$ קיימות כך שגודלן הוא $n$ וסכום איבריהן $a \mod n$ ? נסמן את התשובה ב- $f(n,a)$ .

הבחנה: $f(n,a)$ תלויה רק ב- $n$ וב- $\gcd(n,a)$ . (היוכחו בכך!)

כדי לפתור את השאלה הזו כבר אי-אפשר להשתמש בפיתרון הקומבינטורי, כי לא בטוח ש- $n$ ראשוני. הגישה האלגברית האחרונה כן תעבוד, אבל החישובים יהיו מסובכים יותר כעת.

בינתיים לא אחשוף את התוצאה הסופית, אלא רק שני מקרים פרטים שנקבל:

$f(n,0) = \frac{1}{n} \sum_{d \mid n} \phi(n/d) (-1)^{n+d} \binom{2d}{d}$

$f(n,1) = \frac{1}{n} \sum_{d \mid n} \mu(n/d) (-1)^{n+d} \binom{2d}{d}$

נתחיל. נקודת המוצא שלנו היא (שוב) הפונקציה היוצרת $\prod_{i=1}^{2n} (1+x^i y)$ . המקדם של $x^iy^j$ סופר תתי-קבצות בגודל $j$ עם סכום איברים $i$ . בגלל שמעניין אותנו בסופו של דבר רק סכום איברים מודולו $n$ , אפשר באותה מידה להסתכל דווקא על $F(x,y):= \prod_{i=1}^{n} (1+x^i y)^2$ , וכך נעשה (במקום שהמספרים $i,i+n$ יופיעו, אני מדמיין ש- $i$ מופיע בשני עותקים שונים). אנחנו מעוניינים בסכום המקדמים של המונומים $\{ x^{nk+a}y^n \}_{k \in \mathbb{Z}}$ .

כעת, בעזרת multisection כפול והצבת $x=y=1$ אפשר להביע את סכום המקדמים של המונומים $\{ x^{nk+a}y^{nk'} \}_{k,k' \in \mathbb{Z}}$ . שימו לב שזה יותר מקדמים ממה שאנחנו רוצים (אנחנו רוצים שהמעריך של $y$ יהיה $n$ בדיוק ולא כל כפולה), אבל זו רק בעיה מינורית ונתייחס אליה בהמשך. מקבלים את הסכום הבא:

$S = \frac{1}{n^2} \sum_{1 \le i,j \le n} F(\omega_n^i, \omega_n^j) \omega_n^{-ia} = \frac{1}{n^2} \sum_{1 \le i,j \le n} \prod_{k=1}^{n} (1+\omega_n^{ik} \omega_n^j)^2 \omega_n^{-ia}$

נפשט אותו מעט ע"י כך שנכתוב $(1+\omega_n^{ik} \omega_n^j)^2 = (\omega_n^{-j}+\omega_n^{ik})^2 \omega_n^{2j}$ ונשתמש ב- $\prod_{k=1}^{n} \omega_n^{2j} = ( \omega_n^{2j} )^n = 1$ :

$S = \frac{1}{n^2} \sum_{1 \le i,j \le n} \prod_{k=1}^{n} (\omega_n^{-j}+\omega_n^{ik} )^2 \omega_n^{-ia}$

למה קראתי לזה פישוט בכלל? כי $g_m(x):=\prod_{i=1}^{m} (x+\omega_m^i)=x^m-(-1)^m$ ולכן אפשר לחשב מפורשות את המכפלה $\prod_{k=1}^{n} (\omega_n^{-j}+\omega_n^{ik} ) = g_{n/\gcd(n,i)}(\omega_n^{-j})^{\gcd(n,i)}$ . מקבלים ש-

$S = \frac{1}{n^2} \sum_{1 \le i,j \le n} (\omega_n^{-j n/ \gcd(n,i)} - (-1)^{n/ \gcd(n,i)})^{2 \gcd(n,i)} \omega_n^{-ia}$

בגלל ש- $\omega_{ma}^{a} = \omega_m$ , אפשר לפשט מעט:

$S = \frac{1}{n^2} \sum_{1 \le i,j \le n} (\omega_{ \gcd(n,i) }^{-j} - (-1)^{n/ \gcd(n,i)})^{2 \gcd(n,i)} \omega_n^{-ia}$

עכשיו רואים שהמחובר המתאים ל- $i$ תלוי כמעט רק ב- $\gcd(i,n)$ . על כן, במקום לסכום על $i$ , נסכום על $d$ -ים שמחלקים את $n$ . עם זאת, צריך לקחת בחשבון את שורש היחידה $\omega_n^{-ia}$ שכן תלוי ב- $i$ . בכל אופן, מקבלים:

$S = \frac{1}{n^2} \sum_{1 \le j \le n} \sum_{d \mid n} (\omega_{d}^{-j} - (-1)^{n/d})^{2 d} \sum_{1 \le k \le \frac{n}{d}, \gcd(k,n/d)=1} \omega_n^{-dak}$

יש לנו סכום פנימי על שורשי יחידה, שמגיע ממעבר על כל ה- $i$ -ים שה- $\gcd$ שלהם עם $n$ הוא בדיוק $d$ . אפשר לפשט טיפה את הסכום:

$\sum_{1 \le k \le \frac{n}{d}, \gcd(k,n/d)=1} \omega_n^{-dak} = \sum_{1 \le k \le \frac{n}{d}, \gcd(k,n/d)=1} \omega_{n/d}^{-ak} = \sum_{1 \le k \le \frac{n}{d}, \gcd(k,n/d)=1} \omega_{n/d}^{ak}$

כלומר, אנחנו עוברים על כל שורשי היחידה הפרימטיבים מסדר $n/d$ , מעלים אותם בחזקת $a$ , וסוכמים. לסכום זה יש שם, למען האמת. שמו הוא "סכום רמנוג'אן". נסמן אותו $c_{n/d}(a)$ ונרחיב עליו בהמשך. בינתיים נכתוב את התוצאה שלנו באופן הבא, לאחר שינוי סדר סכימה:

$S = \frac{1}{n} \sum_{d \mid n} c_{n/d}(a) \frac{1}{n} \sum_{j=1}^{n} (\omega_{d}^{-j} - (-1)^{n/d})^{2 d}$

עכשיו מגיע צעד מפתיע: אנחנו מבצעים תהליך הפוך מ-multisection – אנחנו מזהים שהסכום $\frac{1}{n} \sum_{j=1}^{n} (\omega_{d}^{-j} - (-1)^{n/d})^{2 d} = \frac{1}{n} \sum_{j=1}^{n} (\omega_{n}^{-jn/d} - (-1)^{n/d})^{2 d}$ הוא מה שמתקבל לאחר שמבצעים multisection על הפולינום $g_{n,d}(x):=(x^{n/d}-(-1)^{n/d})^{2d}$ , לוקחים את המקדמים במקומות המתחלקים ב- $n$ , וסוכמים.
אפשר לחשב ביטוי זה ישירות, ללא multisection: הפולינום $g_{n,d}$ הוא ממעלה $2n$ . מעניינים אותנו 3 מקדמים שלו: המקדם של $x^0$ (שהוא 1), המקדם של $x^{2n}$ (שהוא גם 1), והמקדם של $x^n$ , שיוצא מהבינום של ניוטון $(-1)^{n+d} \binom{2d}{d}$ . לכן יש לנו ביטוי לסכום:

$S = \frac{1}{n} \sum_{d \mid n} c_{n/d}(a) (2+ (-1)^{n+d} \binom{2d}{d})$

המחובר "2" מעצבן במיוחד, ולשמחתנו מסתבר שאנחנו צריכים להיפטר ממנו – הוא תורם סה"כ $\frac{2}{n} \sum_{d \mid n} c_{n/d}(a) = \frac{2}{n} \sum_{k=1}^{n} \omega_n^{ka} = \frac{2}{n} (n \cdot 1_{n \mid a}) = 2 \cdot 1_{n \mid a}$ .

אם $a \equiv 0 \mod n$ , הוא תורם בדיוק 2 ל- $S$ . אבל אנחנו גם צריכים לחסר 2 מהתוצאה במקרה זה כי $S$ סופרת גם קבוצות בגודל 0 ו- $2n$ (הקבוצה הריקה ו- $\{1,2,\cdots, 2n\}$ ), ואנחנו רוצים רק קבוצות בגודל $n$ .
אם $a \neq 0 \mod n$ , המחובר "2" תורם 0 ל- $S$ . בנוסף, בגלל שסכום האיברים של הקבוצה $\{1,2,\cdots, 2n\}$ ושל הקבוצה ריקה שניהם מתחלקים ב- $n$ (ולא שווים ל- $a \mod n$ ) אין צורך לעשות איזשהו תיקון ל- $S$ .

בשני המקרים, מקבלים שהפיתרון לבעיית הספירה המוכללת שלנו הוא:

$f(n,a) = \frac{1}{n} \sum_{d \mid n}c_{\frac{n}{d}}(a) (-1)^{n+d} \binom{2d}{d}$

עד כמה שאני יודע, זו תוצאה מקורית של בעל הבלוג 🙂
יתכן ואתם לא מרוצים מהנוסחה, כי היא משתמשת באותם "סכומי רמנוג'אן", סכום על שורשי יחידה פרימיטיבים המועלים בחזקה כלשהי. נראה שלפחות בשני המקרים הכי מעניינים הם בעצם ניתנים לחישוב מפורש:

$a=0$ : סכום רמנוג'אן $c_{\frac{n}{d}}(a)$ נהיה $\sum_{1 \le k \le \frac{n}{d}, \gcd(k,n/d)=1} 1 = \phi(n/d)$ , ומקבלים את הנוסחה $f(n,0) = \frac{1}{n} \sum_{d \mid n} \phi(n/d) (-1)^{n+d} \binom{2d}{d}$ . עבור $n=p$ ראשוני אי-זוגי נקבל את הבעיה השישית של IMO 1995.
$a=1$ : סכום רמנוג'אן $c_{\frac{n}{d}}(a)$ נהיה $\sum_{1 \le k \le n/d, \gcd(k, n/d)=1} \omega_{n/d}^k$ . הוא שווה ל- $\mu(n/d)$ , פונקציית מביוס. דרך אחת לראות זאת היא להסתכל על כל הסכומים הללו בו"ז: נסמן $S_m := \sum_{1 \le k \le m, \gcd(m,k)=1} \omega_{m}^k$ , ונבחין כי $\sum_{d \mid n} S_d = \sum_{k=1}^{n} \omega_n^k = \delta_{n,1}$ , וזו בדיוק התכונה המגדירה של פונקציית מביוס. לכן פיתרון בעיית הספירה נהייה $f(n,1) = \frac{1}{n} \sum_{d \mid n} \mu(n/d) (-1)^{n+d} \binom{2d}{d}$ .

כעת אעיר כמה הערות חשובות על הנוסחה:

מהפיתרון הכללי רואים שהפירוק של $n$ קריטי לחישוב – יש מחובר לכל מחלק של $n$ .
נניח ש- $n$ אי-זוגי. הנוסחה נהיית $f(n,a) = \frac{1}{n} \sum_{d \mid n}c_{\frac{n}{d}}(a) \binom{2d}{d}$ . בגלל ש- $c_{n/d}(a) \le \phi(n/d)$ , עם שיוויון אמ"מ $a \equiv 0 \mod {n/d}$ , נובע: המקסימום של $f(n,a)$ (עבור $n$ אי-זוגי קבוע) מתקבל ב- $a =0$ . כלומר, אם נסתכל על תתי-קבוצות בגודל $n$ של $\{1,2,\cdots,2n\}$ , נסכום את האיברים ונסתכל מודולו $n$ , נקבל שהשארית 0 היא הכי נפוצה. האם יש דרך להוכיח את זה בלי לעבור דרך הנוסחה המפורשת? כמו כן, מה קורה במקרה הזוגי? מה המקסימום אז?
גם במקרים $a\neq 0,1$ יש ביטוי סגור לסכומי רמנוג'אן, המערב ביחד גם את פונקציית אוילר וגם את פונקציית מביוס. הביטוי הוא $c_n(a) = \mu(n/(n,a)) \frac{\phi(n)}{\phi(n/(n,a))}$ . ההוכחה לכך מופיע כתרגיל 11 במסמך "פונקציות אריתמטיות" שכתבתי. שימו לב שהסימונים שונים מהסימונים בפוסט הזה. אנחנו שוב רואים שהפירוק של $n$ מהותי, כי סכומי רמנוג'אן מחושבים בעזרת פונקציות כפליות שתלויות בפירוק של $n$ .

שאלתי את R. Stanley האם הוא נתקל בסכומים כאלה. הוא ציין סכום עם אופי דומה שהופיע במאמר שלו על קודים לתיקון שגיאות. גם שם ההוכחה הייתה אלגברית, וב-Remark 1 בעמוד הרביעי מחברי המאמר העלו את השאלה: האם קיימת הוכחה קומבינטורית לנוסחה שלהם? אני מעלה את אותה השאלה בהקשר של בעיית הספירה שהוכחתי עם פונקציות יוצרות. אפילו שהתוצאה הסופית – במיוחד במקרה $a=1$ – מזכירה הכלה-הדחה בצורתה, הדרך שבא הגענו אליה הייתה אלגברית מאוד.

שאלה פתוחה לקוראים: האם אפשר להוכיח את הנוסחה ל- $f(n,a)$ קומבינטורית ל- $n$ כללי? אפילו המקרים $a=0,1$ מעניינים.

לפני שעוברים לדבר הבא, תרגיל פרי עטי:

תרגיל: הראו שהשונות של $f(n,a)$ היא $\frac{\sum_{d \mid n, d \neq n} \binom{2d}{d}^2 \phi(\frac{n}{d})}{n^2}$ .

3. Wolstenholme (טיזר)

על זה אדבר רק בפוסט הבא, מה זה עושה פה?
כאתגר לקוראים, אשאיר לכם לנסות להוכיח (ולהכליל) את הקונגרואנציה הבאה, עבור $p$ ראשוני גדול מ-3:

$\binom{2p}{p} \equiv 2 \mod {p^3}$

בתקווה שלא תשכחו את כל זה עד הפוסט הבא,
למרות שלא נורא אם כן,
אופיר

נ.ב. אשמח לתגובות, כתמיד 🙂